Binary classification

2017 · Machine Learning

Github Repo

Problem description:

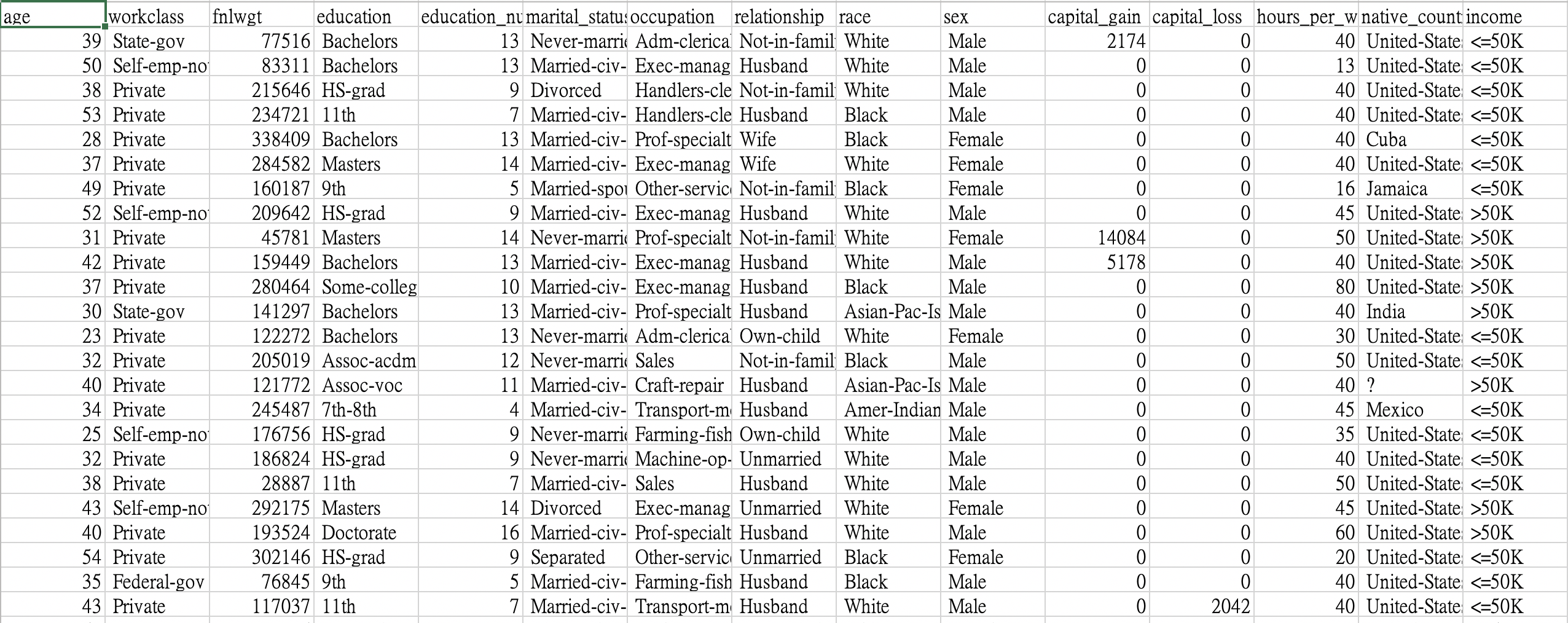
Determine whether a person makes over 50K a year

Logistic regression

• Logistic regression is a statistical model that in its basic form uses a logistic function to model a binary dependent variable
• Step 1: Function Set $$f_{w,b}(x) = \sigma\left(\sum_i w_i x_i+b\right)$$ Sigmoid function: $$\sigma(z)=\frac{1}{1+e^{-z}}$$
• Step 2: Goodness of a Function Training data: $(x^n,\hat(y)^n)$ $$L(f)=\sum_n C(f(x^n),\hat(y)^n)$$
• Step 3: Find the best function $$w_i\leftarrow w_i-\eta\sum_n \left(\hat(y)^n-f_{w,b}(x^n)\right)x^n_i$$

Generative model

• In General, A Discriminative model ‌models the decision boundary between the classes. A Generative Model ‌explicitly models the actual distribution of each class.
• Step 1: Find $\mu_1, \mu_1, \Sigma_1, \Sigma_2$
• Step 2: Compute the corresponding $w,b$ $$w^T=(\mu_1-\mu_2)^T\Sigma^{-1}$$ $$b=-\frac{1}{2}(\mu_1)^T(\Sigma_1)^{-1}\mu_1+\frac{1}{2}(\mu_2)^T(\Sigma_2)^{-1}\mu_2+\text{ln}\frac{N_1}{N_2}$$

Result

• Achieved 97/402 (Top $25\%$) rank in the Kaggle competition