Matrix Factorization

2017 · Machine Learning

Github Repo

Problem description:

• Given the user’s rating history on items, we want to predict the rating of unseen (user, item) pairs.
• Implement matrix factorization to predict the missing value on the user-item matrix.

	涼宮春日的憂鬱	4月是你的謊言	科學超電磁砲
大木博士	5	N/A	4
小智	N/A	3	N/A
小茂	2	N/A	2
吸盤魔偶	4	2	N/A

Matrix Factorization

• \[R\approx \hat{R}=U\cdot V^T\]

where $R$ is a sparse matrix with $n$ users and $m$ movies

$U$: a $(n\times d)$ dimension matirx

$V^T$: a $(d\times m)$ dimension matrix

• Minimize loss function by gradient descent

\[L=\sum_{i,j}(R_{ij}-U_i\cdot V_j)^2\]

• Bias term

\[r_{ij}=U_i\cdot V_j+b_i^{user}+b_j^{movie}\]

Functions in Keras

1. keras.layers.Embedding: the user matrix and item matrix can be viewed as two embedding matrix
2. keras.layers.Flatten: the output tensor shape of the embedding layer would be [batch_size,1,embedding_dim], you need this function to reshape the tensor to [batch_size,embedding_dim]
3. keras.layers.Dot: if applied to two tensors a and b of shape (batch_size, n), the output will be a tensor of shape (batch_size, 1) where each entry i will be the dot product between a[i] and b[i].
4. keras.layers.Add: add all tensors
5. keras.layers.Concatenate: concatenate two tensors

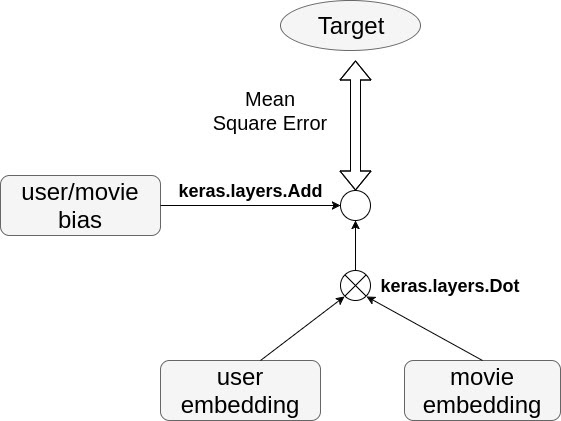
Result

• Achieved 55/335 (Top $17\%$) rank in the Kaggle competition