Reinforcement Learning

2018 · Machine Learning

Github Repo

Policy gradient

• Play an Atari game (Pong) using deep reinforcement learning

• Algorithm:

  • Update per step $t$: $\theta \leftarrow \theta+\alpha\nabla_\theta \log \pi_\theta (s_t, a_t) v_t$
    

    $s_t$: state, $a_t$: action, $v_t$: long-term value, $\pi_\theta(s,a) = P[a|s, \theta]$

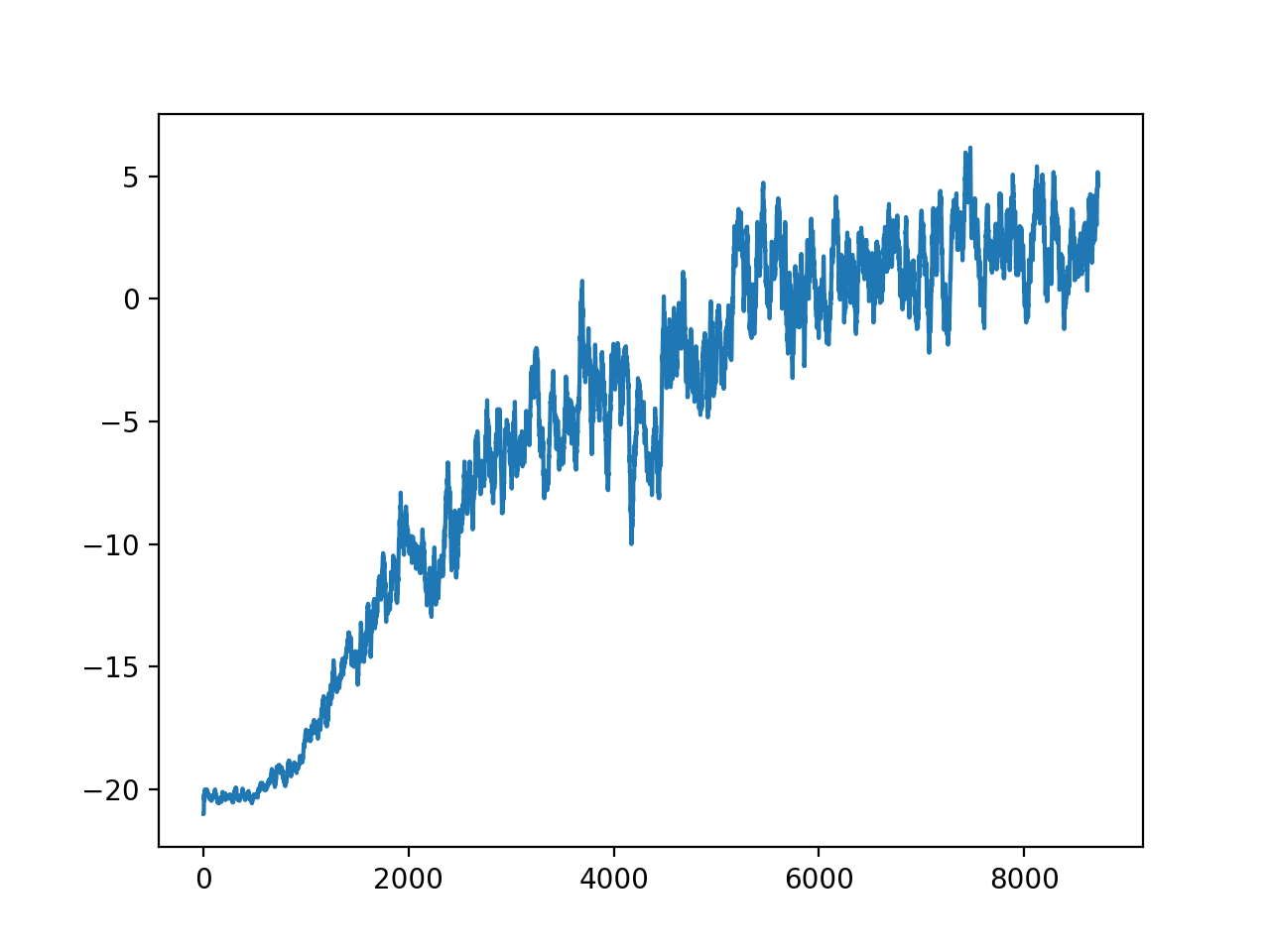
• Result: Baseline: 3 points

Deep Q Learning

• Environment: Breakout

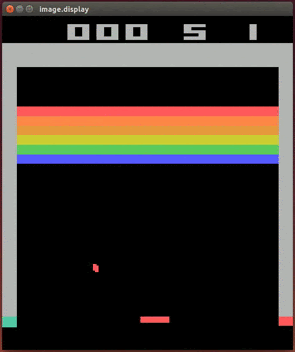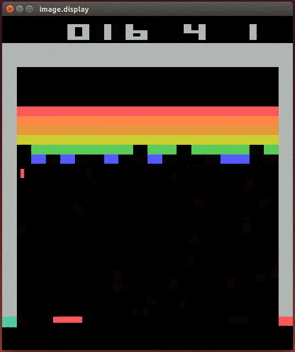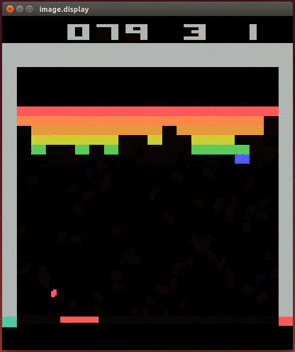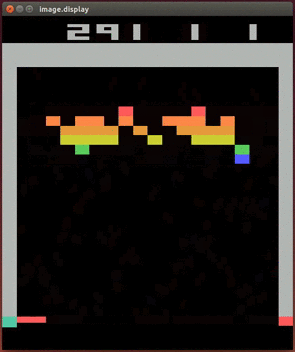
• Algorithm:
  1. Take some action $a_i$ and observe $(s_i, a_i, s_i’, r_i)$, add it to $\mathcal{B}$ (replay buffer)
  2. Sample mini-batch ${s_j, a_j, s_j’, r_j}$ from $\mathcal{B}$ uniformly
  3. Compute $y_j = r_j+\gamma\text{max}_{a_j’}Q_{\phi’}(s_j’,a_j’)$ using target network $Q_{\phi’}$
  4. $\phi\leftarrow\phi-\alpha\sum_j\frac{dQ_{\phi’}}{d\phi}(s_j, a_j)(Q_\phi (s_j, a_j)-y_j)$
  5. Update $\phi’$: copy $\phi$ every $N$ steps
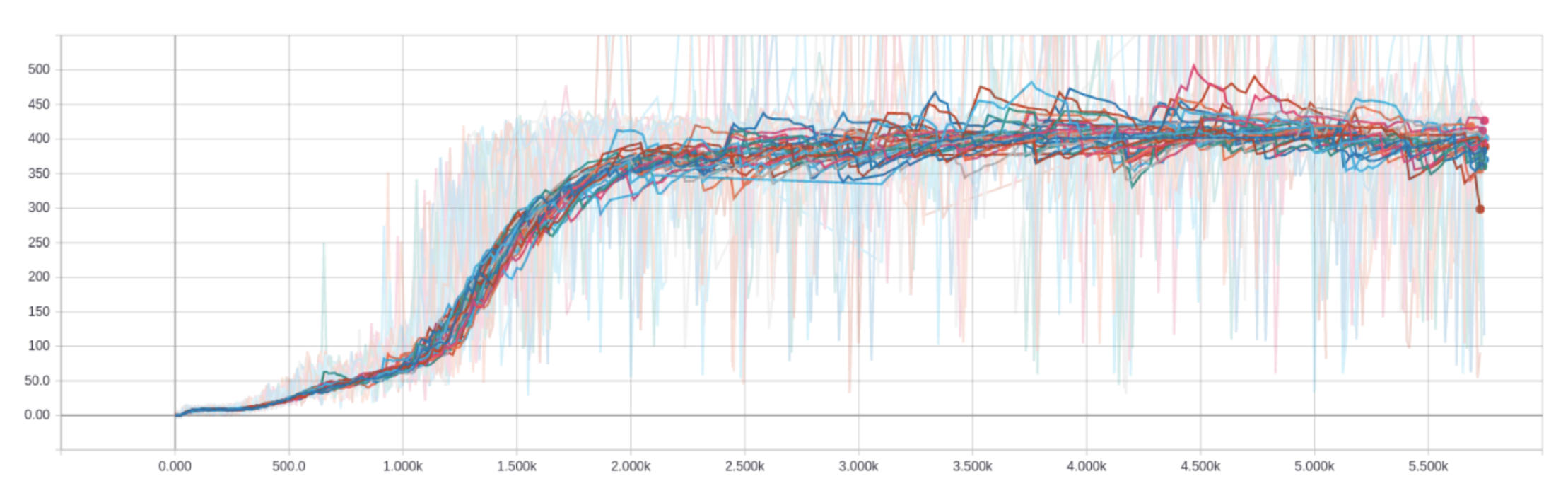
• Result: Baseline: 40 points

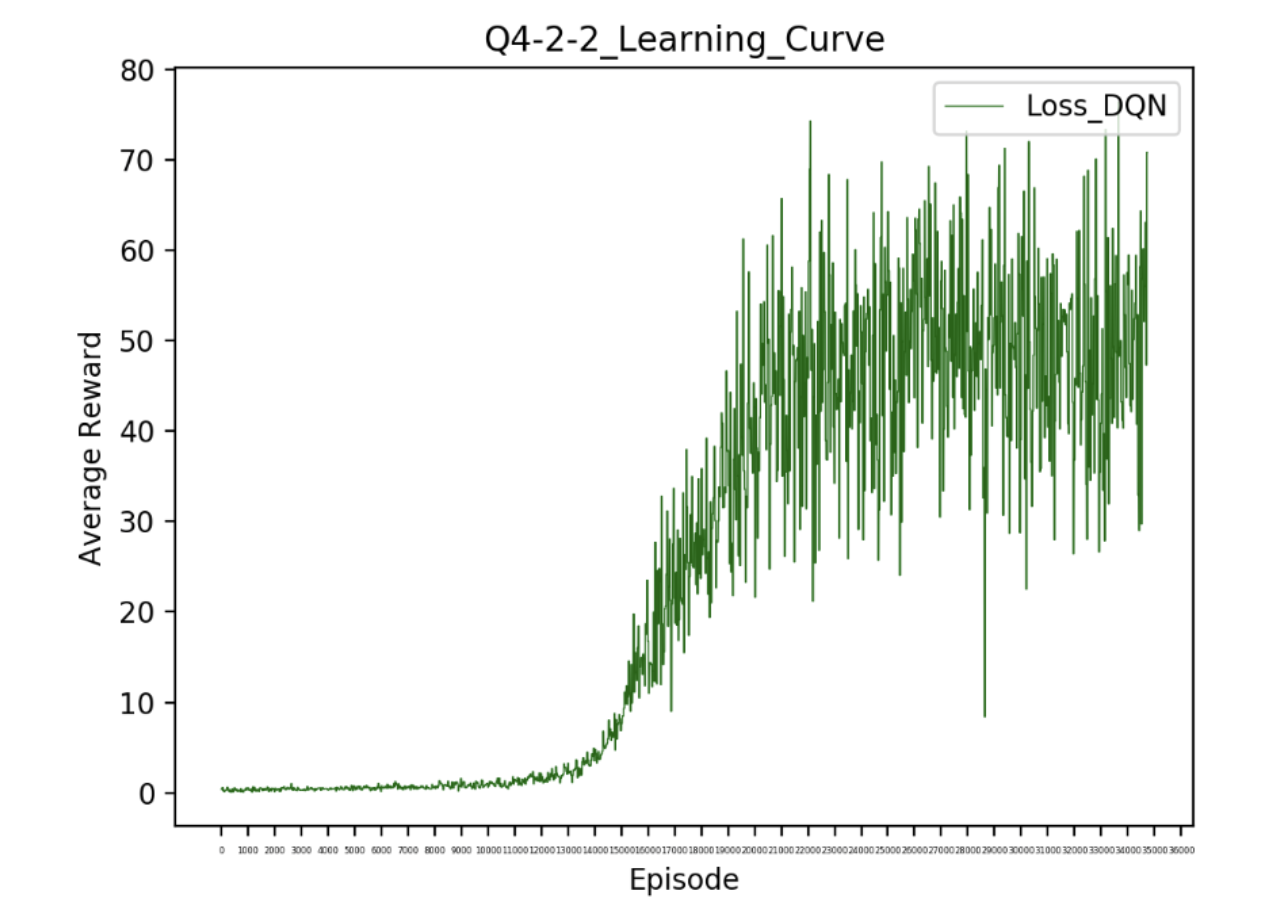
• Comparison between DQN and DDQN

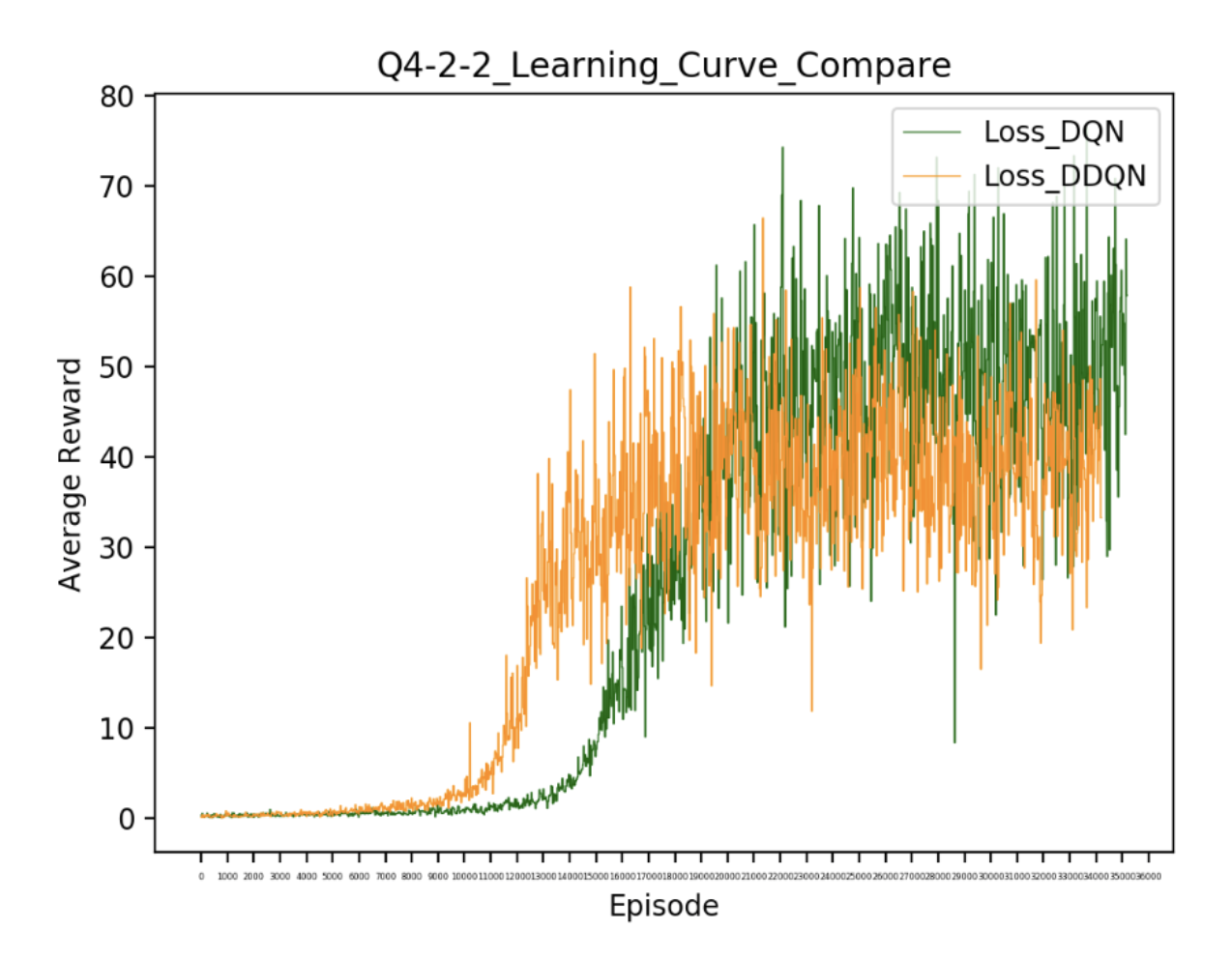
Actor-Critic

• Environment: Pong, Breakout
• Algorithm:
  1. Take an action $a~\pi_\theta(a|s)$, get $(s,a,s’,r)$
  2. Update $\hat{V}_\phi^{\pi}$ using target $r+\gamma\hat{V}_\phi^{\pi}(s’)$
  3. Evaluate $\hat{A}^{\pi}(s,a)=r(s,a)+\gamma\hat{V}_\phi^{\pi}(s’)-\hat{V}_\phi^{\pi}(s)$
  4. $\nabla_\theta J(\theta)\approx \nabla_\theta\log \pi_\theta (a|s) \hat{A}^\pi (s,a)$
  5. $\theta\leftarrow \theta + \alpha \nabla_\theta J(\theta)$
• Result:
  • A2C: Pong

  

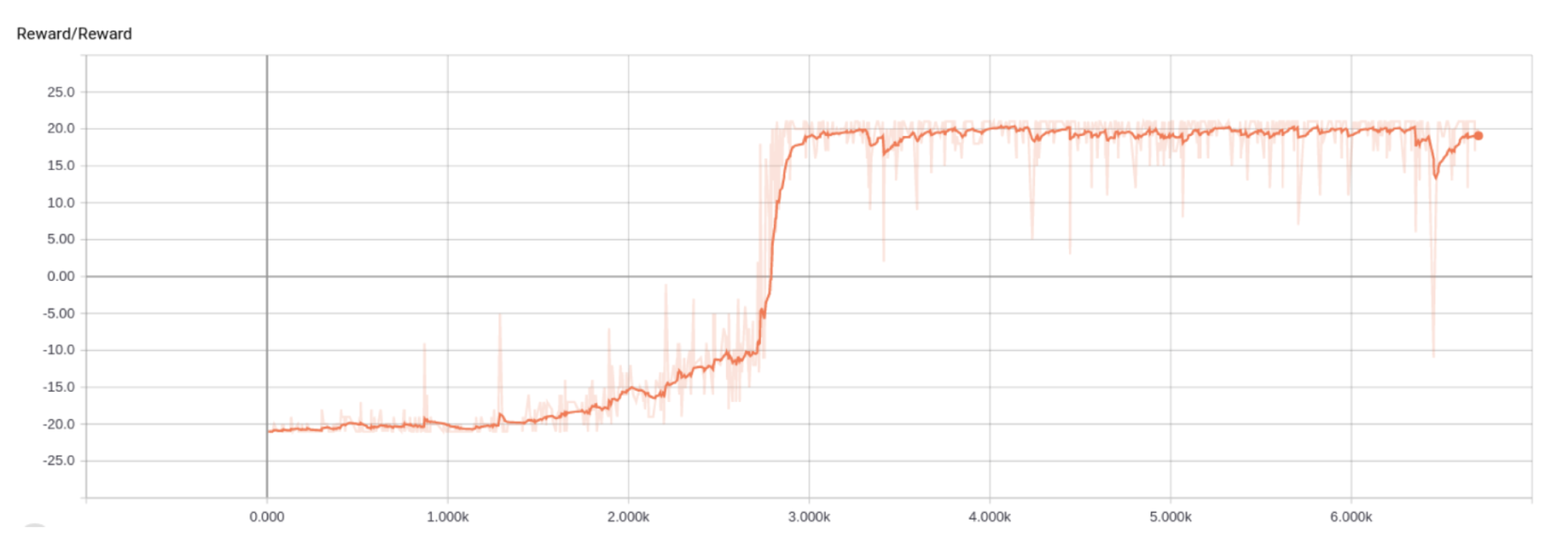
  • A2C: Breakout

  

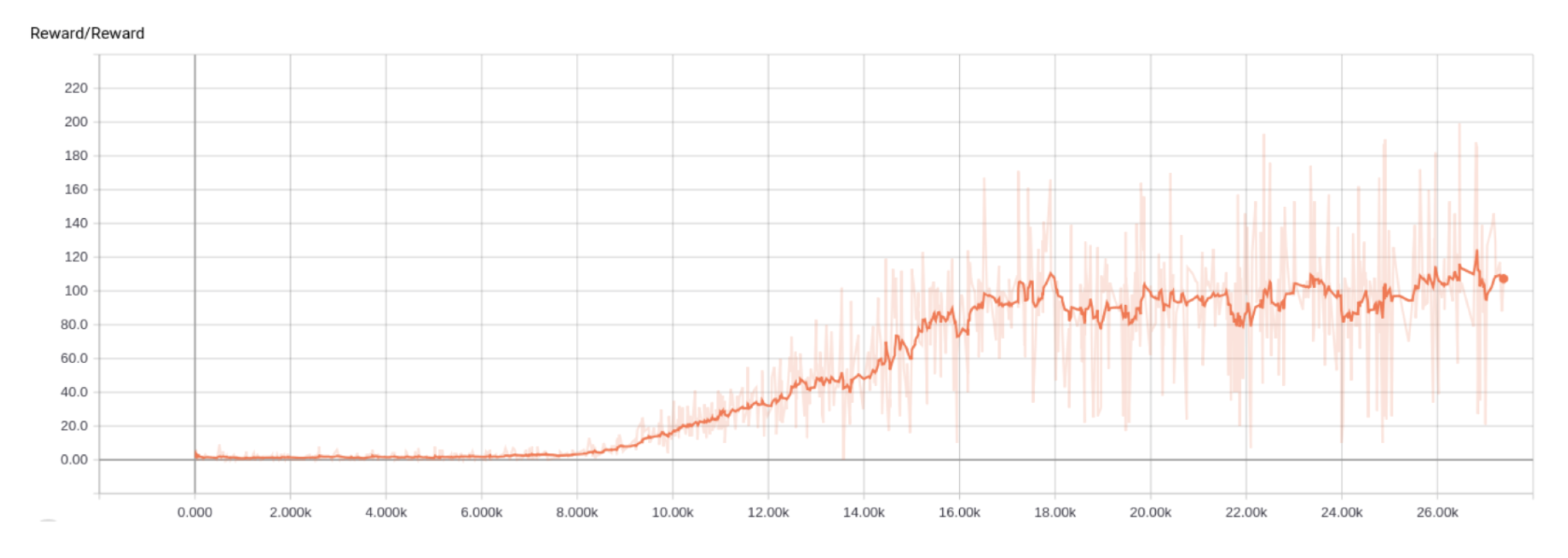
  • ACKTR: Pong

  

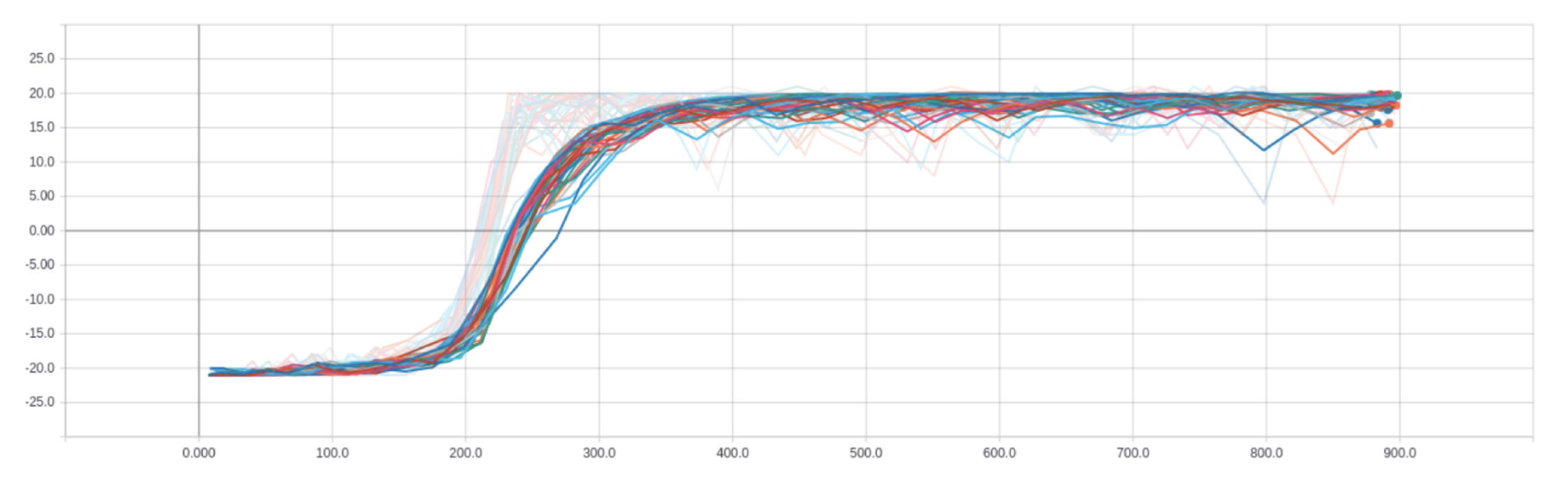
  • ACKTR: Breakout